AVL Tree

AVL 是最早被发明的自平衡二叉搜索树，它的名字是以其两位发明者 Georgy Adelson-Velsky 和 Evgenii Landis 来命名的，他们在1962年的论文 An information for the information of information 中发表了它。

AVL 本质上还是一颗BST，其特点:

满足BST的定义
任意节点的两个子树的高度差最多为1
搜索、插入、删除操作在平均情况和最坏情况下都为O(log n)

插入节点或删除节点会造成树的不平衡，因此需要旋转操作来保持树的平衡。

Balance factor(平衡因子)

在二叉树中一个节点N的平衡因子被定义为两个子树的差:

BalanceFactor(N) = Height(RightSubtree(N)) - Height(LeftSubtree(N))

因此AVL树任意节点的平衡因子只能为 -1、0 或 1。

对于一个节点N:

BalanceFactor(N) < 0 => 称该节点 left-heavy
BalanceFactor(N) > 0 => 称该节点 right-heavy
Balancefactor(N) = 0 => 称该节点 balanced

AVL 涉及以下四种旋转（假设X为rebalancing前临时平衡因子为-2或2的节点）:

Right Right (RR) => Z 为 X 的右孩子且 BalanceFactor(Z) >= 0
Left Left (LL)   => Z 为 X 的左孩子且 BalanceFactor(Z) <= 0
Right Left (RL)  => Z 为 X 的右孩子且 BalanceFactor(Z) == -1
Left Right (LR)  => Z 为 X 的左孩子且 BalanceFactor(Z) == +1

其中前两种为Simple Rotation，后两种为 Double Rotation(需要进行两次旋转)。

以RR为例说明Simple Rotation:

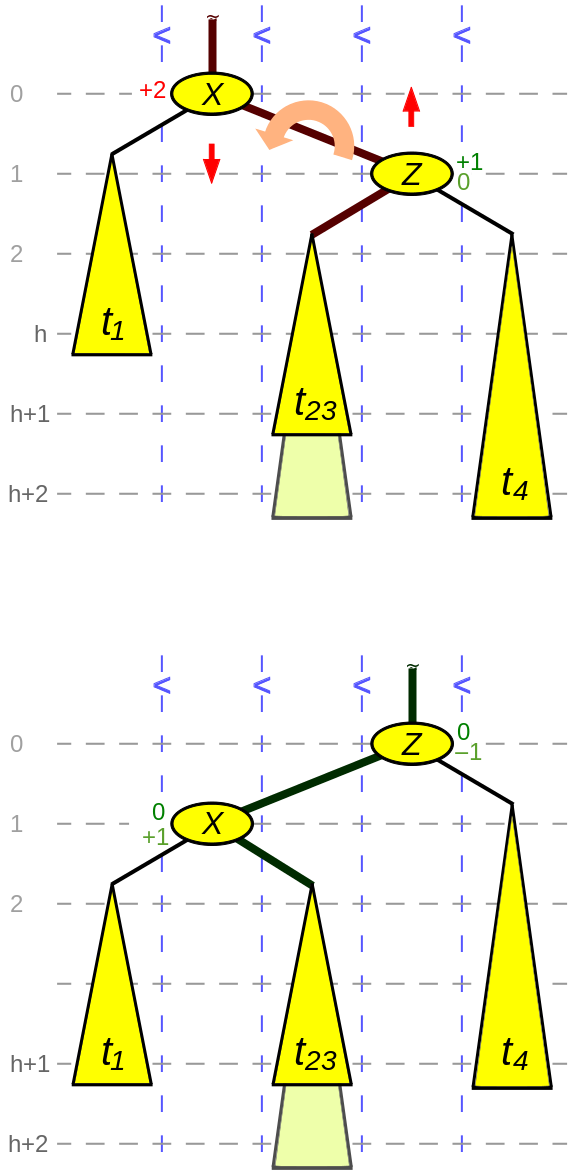
Simple rotation

因为在Z的左子树删除了节点或在Z的右子树增加了新的节点，导致了X的平衡因子变为+2，且X的平衡因子为+1(right-heavy)，因此需要进行左旋转，Z变为根节点，Z的左子树变为X的右子树，X变为Z的左子树（依然满足BST的条件）。伪代码如下:

node *rotate_left(node *X, node *Z) {
    // Z节点的比其兄弟节点高2个单位
    t23 = Z -> left_child;
    X -> right_child = t23;

    if (t23 != null) {
        t23 -> parent = X;
    }

    Z -> left_child = X;
    X -> parent = Z;

    // 第一种情况，BalanceFactor(Z) == 0, 只发生在删除节点的时候
    if (BalanceFactor(Z) == 0) { // t23 与 t4 一样高
        BalanceFactor(X) = +1;   // t23 高了
        BalanceFactor(Z) = -1;   // t4 矮了
    } else { // 第二种情况，插入或删除都可出现该种情况
        BalanceFactor(X) = 0;
        BalanceFactor(Z) = 0; 
    }

    return Z;   // 返回旋转后的根节点
}

以RL为例说明Double Rotation:

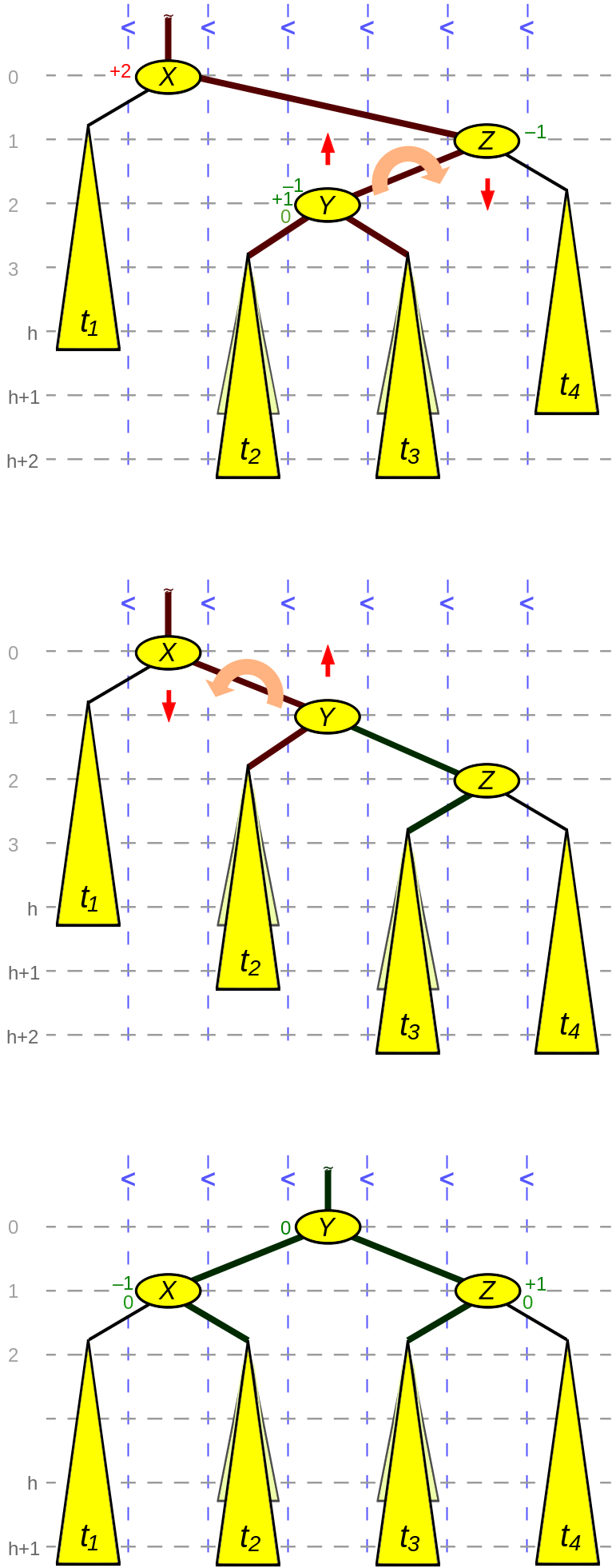
Double rotation

不同于RR，RL的Z节点的平衡因子为-1，即Z是left-heavy的，此时应该先对Z和Y进行一次右旋转，然后再对X和Z进行坐旋转。伪代码如下:

node *rotate_right_left(node *X, node *Z) {
    // Z节点的比其兄弟节点高2个单位
    Y = Z -> left_child;
    // Y节点的比其兄弟节点高1个单位
    t3 = Z -> right_child;
    if (t3 != null) {
        t3 -> parent = Z;
    }
    Y -> right_child = Z;
    Z -> parent = Y;
    X -> right_child = Y;   // 该步可省略
    Y -> parent = X;        // 该步可省略

    // 以上完成第一次旋转

    t2 = Y -> left_child;
    X -> right_child = t2;

    if (t2 != null) {
        t2 -> parent = X;
    }

    Y -> left_child = X;
    Y -> parent = X -> parent;  // X的父亲现在成为Y的父亲
    X -> parent = Y;

    // 第一种情况, 插入或删除都会出现该情况
    if (BalanceFactor(Y) > 0) { // t3 以前较高
        BalanceFactor(X) = -1   // t1 现在更高
        BalanceFactor(Z) = 0;
    } else if (BalanceFactor(Y) == 0)  { // 第二种情况只出现在删除时
        BalanceFactor(X) = 0;
        BalanceFactor(Z) = 0;
    } else { // 第三种情况可能出现在插入或删除的情况
        BalanceFactor(X) = 0;   // t2 以前更高
        BalanceFactor(Z) = +1;  // t4 现在更高
    }

    BalanceFactor(Y) = 0;

    return Y;   // 返回旋转后新的根节点
}

AVL C++ 实现给出了不同于上述伪代码的实现，使用树的高度来判断是否需要重新平衡。

Reference:
1 AVL_tree